4. Median of Two Sorted Arrays
Method 1: Merge 2 sorted arrays and get the median easily
class Solution0:
"""
Runtime: 104 ms, faster than 56.39% of Python3 online submissions for Median of Two Sorted Arrays.
Memory Usage: 14.1 MB, less than 33.79% of Python3 online submissions for Median of Two Sorted Arrays.
"""
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
arr, i, j = [], 0, 0
# merge 2 sorted array
while i < len(nums1) and j < len(nums2):
if nums1[i] < nums2[j]:
arr.append(nums1[i])
i += 1
else:
arr.append(nums2[j])
j += 1
if i < len(nums1):
arr.extend(nums1[i:])
elif j < len(nums2):
arr.extend(nums2[j:])
total_len = len(arr)
mid = total_len // 2
# get median depending on whether total number is odd or even
if total_len % 2 == 1:
return arr[mid]
else:
return (arr[mid - 1] + arr[mid]) / 2
Analysis
Assuming len(nums1) = m, len(nums2) = n
Time Complexity:
- Merge takes of time, getting median takes of time
Space Complexity:
- Need to store an extra array
Method 2: Find partition with binary search
class Solution:
"""
Runtime: 88 ms, faster than 95.63% of Python3 online submissions for Median of Two Sorted Arrays.
Memory Usage: 14.2 MB, less than 22.35% of Python3 online submissions for Median of Two Sorted Arrays.
"""
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
nums1_len, nums2_len = len(nums1), len(nums2)
if nums1_len > nums2_len:
return self.findMedianSortedArrays(nums2, nums1)
low, high = 0, nums1_len
while low <= high:
# select a partition in nums1
p1 = (low + high) // 2
# select a partition in nums2 based on the previous partition
p2 = (nums1_len + nums2_len + 1) // 2 - p1
max1 = -float("inf") if p1 == 0 else nums1[p1 - 1]
max2 = -float("inf") if p2 == 0 else nums2[p2 - 1]
min1 = float("inf") if p1 == nums1_len else nums1[p1]
min2 = float("inf") if p2 == nums2_len else nums2[p2]
if max1 <= min2 and max2 <= min1: # partition satisfied
if (nums1_len + nums2_len) % 2 == 1:
return max(max1, max2)
else:
return (max(max1, max2) + min(min1, min2)) / 2
elif max1 > min2: # binary search left
high = p1 - 1
else: # binary search right
low = p1 + 1
Explanation
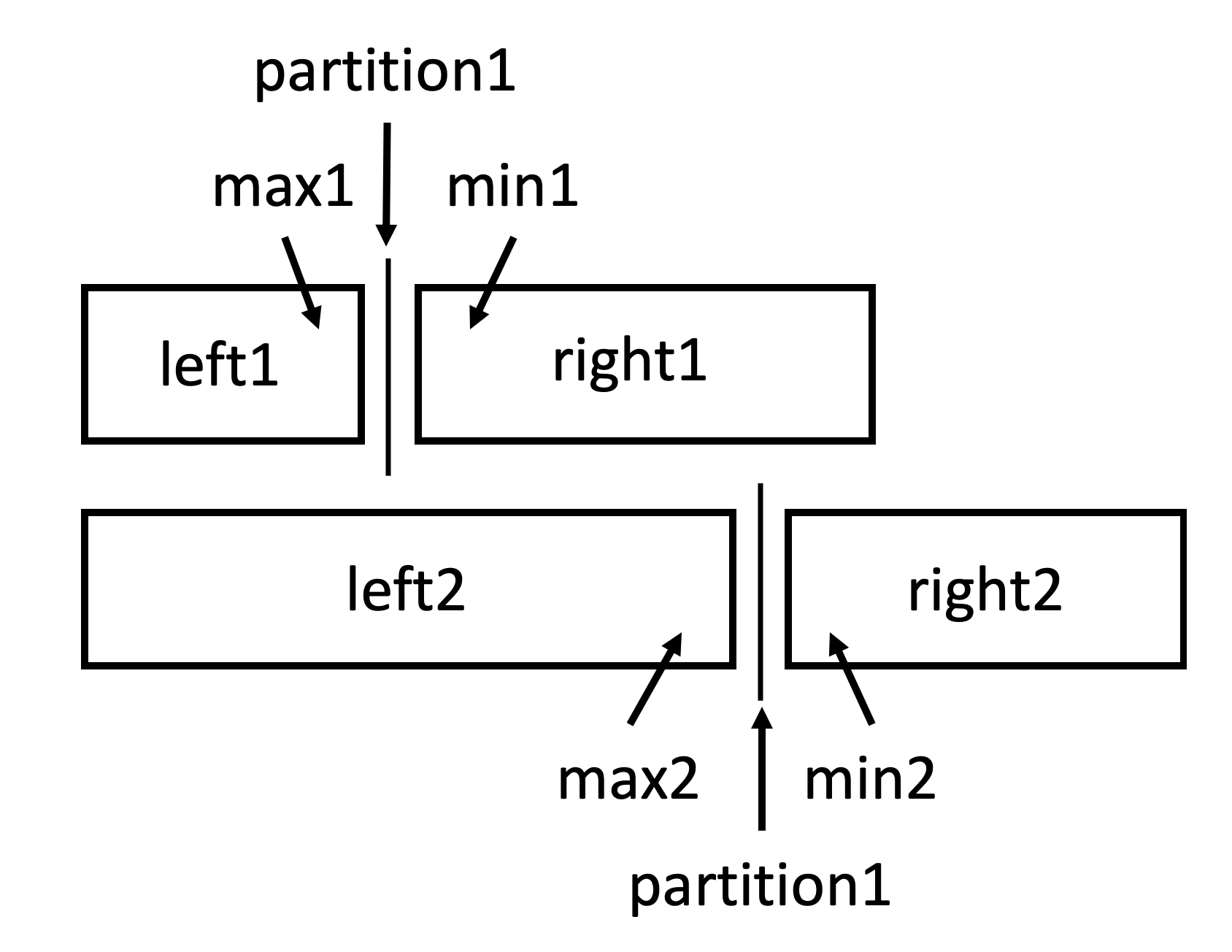
Make a partition in nums1 such that len(left1)+len(left2)==len(right1)+len(right2) (if total number of 2 arrays is odd, then len(left1)+len(left2)==len(right1)+len(right2)+1, the left partition has 1 more element than the right partition) (Condition1)
Partition1 is selected with binary search, partition2 is selected based on partition1 to make sure Condition1 is satisfied.
The condition to exit is max1>min2 && max2>min1, in this case, everything on the left is smaller than everything on the right. Then the median must be around the 2 partitions.
-
Case 1: Total number is Odd
Since the total of the left partition is 1 more than the total of the right partition, the median is the max in the left partition. The max is either
max1ormax2. -
Case 2: Total number is Even
The median would be the average of the max in the left partition and the min in the right partition, which is
(max(max1, max2) + min(min1, min2)) / 2.
If Condition1 is not satisfied, then keep searching for the right partition with binary search. That is, if max1 > min2 (partition1 too high), then binary search in left1, else, binary search in right1.
Analysis
Assuming len(nums1) = m, len(nums2) = n
Time Complexity:
- Binary Search on the shorter array
Space Complexity:
- Store constant number of variables.