6. ZigZag Conversion
Question
Example
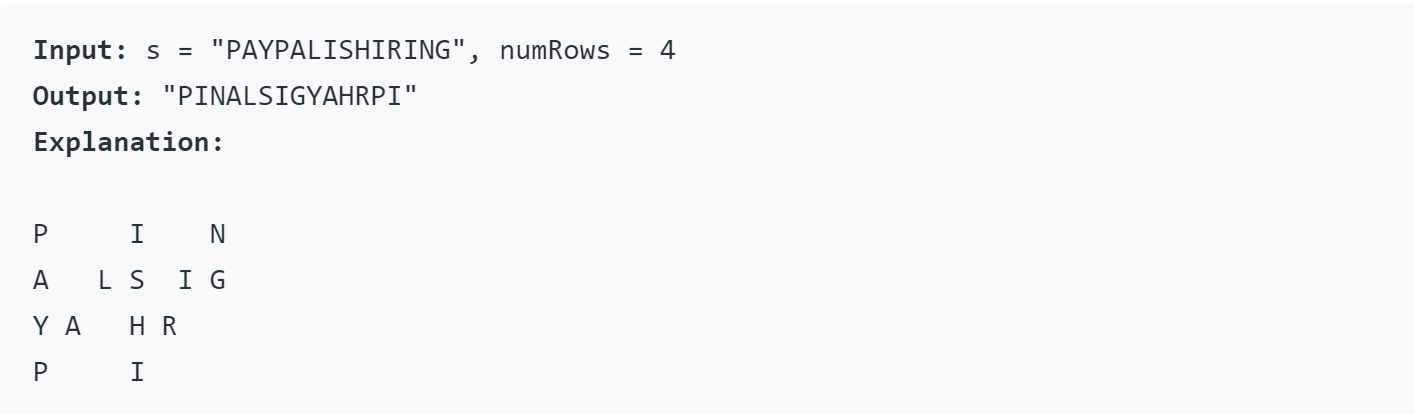
Trivial Solution (But Complex Implementation)
Put the string into a 2D table, and sum (concatenate) the rows where there's a letter.
/**
* Runtime: 64 ms, faster than 23.23% of C++ online submissions for ZigZag Conversion.
* Memory Usage: 19.7 MB, less than 12.30% of C++ online submissions for ZigZag Conversion.
*/
class Solution
{
public:
int num_col(int s_len, int numRows)
{
if (numRows == 1)
return s_len;
int size_v = 2 * numRows - 2;
int num_v = s_len / size_v;
int num_v_col = numRows - 1;
int extra_letter = s_len % size_v;
int extra_col = extra_letter > 0 ? 1 : 0;
if (extra_letter - numRows > 0)
{
extra_col += extra_letter - numRows;
}
int num_col = num_v * num_v_col + extra_col;
return num_col;
}
string convert(string s, int numRows)
{
// calculate num column
int s_len = s.length();
int num_col = this->num_col(s_len, numRows);
vector<vector<char>> table(numRows, vector<char>(num_col, '\0'));
short vertical_index = -1, horizontal_index = 0, direction = 1;
for (unsigned int i = 0; i < s_len; i++)
{
// calculate horizontal index
horizontal_index = this->num_col(i + 1, numRows) - 1;
if (vertical_index + direction < 0 || vertical_index + direction >= numRows)
{
direction = -direction;
}
if (numRows == 1)
vertical_index = 0;
else
vertical_index += direction;
table[vertical_index][horizontal_index] = s[i];
}
// collect result
string result = "";
for (int row = 0; row < numRows; row++)
{
for (int col = 0; col < num_col; col++)
{
if (table[row][col] != '\0')
{
result += table[row][col];
}
}
}
return result;
}
};
Complexity Analysis
Assuming
- Time Complexity: (Iterate through 2D Table)
- Space Complexity: (2D Table)
Official Solution
Approach 1: Sort by Row
Intuition
By iterating through the string from left to right, we can easily determine which row in the Zig-Zag pattern that a character belongs to.
Algorithm
We can use lists to represent the non-empty rows of the Zig-Zag Pattern.
Iterate through from left to right, appending each character to the appropriate row. The appropriate row can be tracked using two variables: the current row and the current direction.
The current direction changes only when we moved up to the topmost row or moved down to the bottommost row.
/**
* Runtime: 32 ms, faster than 56.09% of C++ online submissions for ZigZag Conversion.
* Memory Usage: 10.4 MB, less than 44.71% of C++ online submissions for ZigZag Conversion.
*/
class Solution1
{
public:
string convert(string s, int numRows)
{
if (numRows == 1)
return s;
vector<string> rows(min(numRows, int(s.length())));
int cur_row = 0, direction = -1;
for (char c : s)
{
rows[cur_row] += c;
if (cur_row == 0 || cur_row == numRows - 1)
direction = -direction;
cur_row += direction;
}
string result;
for (string row : rows)
result += row;
return result;
}
};
Complexity Analysis
- Time Complexity: , where
- Space Complexity:
Approach 2: Visit by Row
Intuition
Visit the characters in the same order as reading the Zig-Zag pattern line by line.
Algorithm
Visit all characters in row 0 first, then row 1, then row 2, and so on...
For all whole numbers ,
- Characters in row 0 are located at indexes
- Characters in row (last row) are located at indexes
- On each inner row, there are 2 letters in each cycle
- Characters in inner row are located at indexes
- and
/**
* Runtime: 16 ms, faster than 97.93% of C++ online submissions for ZigZag Conversion.
* Memory Usage: 8.1 MB, less than 71.90% of C++ online submissions for ZigZag Conversion.
*/
class Solution2
{
public:
string convert(string s, int numRows)
{
if (numRows == 1)
return s;
string ret;
int n = s.size();
int cycleLen = 2 * numRows - 2;
for (int i = 0; i < numRows; i++)
{
// iterate through each row
for (int j = 0; j + i < n; j += cycleLen)
{
// jump to the next cycle position
ret += s[j + i]; // responsible for the outer rows and inner rows going down
if (i != 0 && i != numRows - 1 && j + cycleLen - i < n)
{
// inner rows
ret += s[j + cycleLen - i]; // responsible for the inner rows going up
}
}
}
return ret;
}
};
Explanation
The ret += s[j + cycleLen - i]; may be confusing.
Outer Rows (First Row/Last Row)

Inner Rows


Complexity Analysis
- Time Complexity: , where . Each index is visited once.
- Space Complexity: . For the cpp implementation, if return string is not considered extra space.