11. Container With Most Water
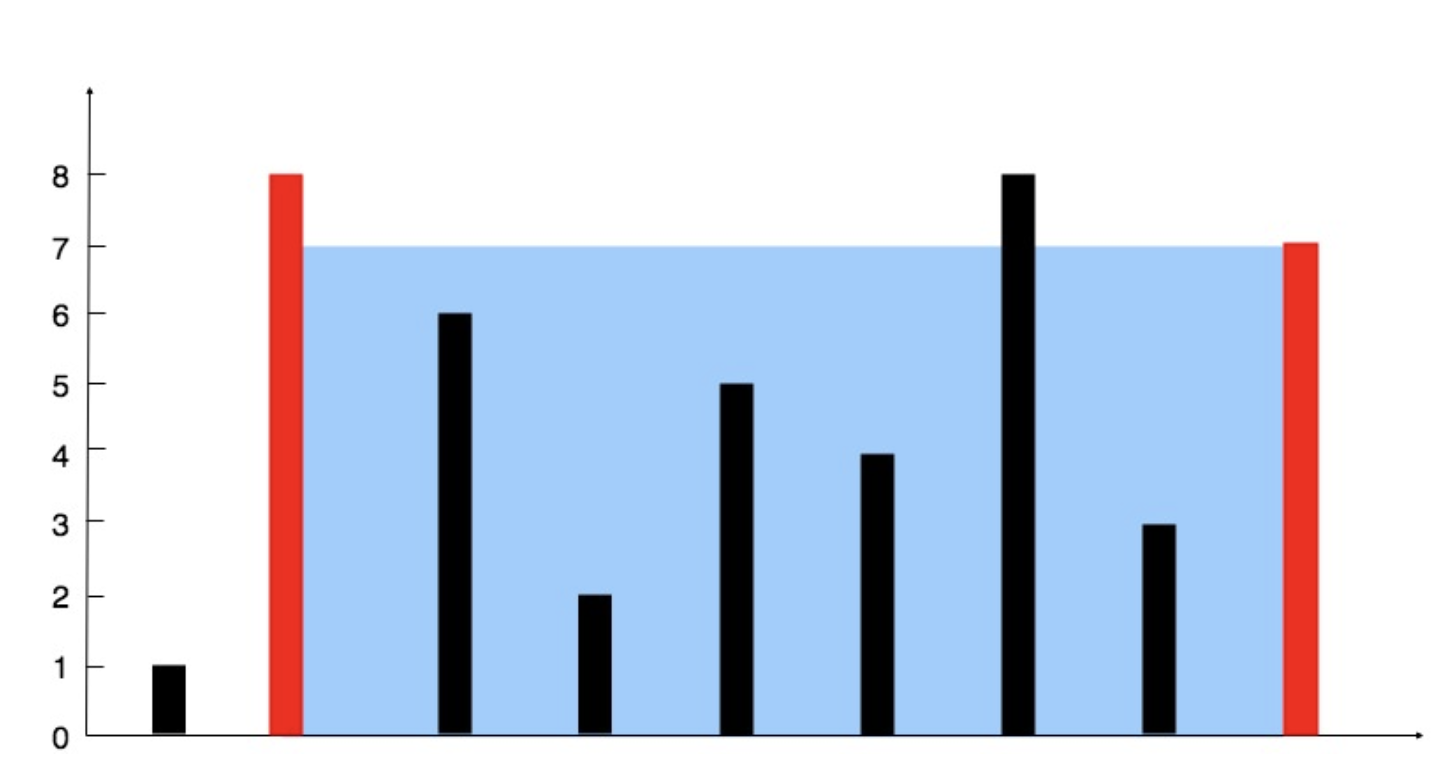
Area 由宽度和高度决定,宽度是 2 条线的差,高度是当前 2 个指针的 min。
Brute Force
列出所有组合。
Time Complexity:
Space Complexity:
Python Implementation
class Solution:
def maxArea(self, height: List[int]) -> int:
m = 0
for i in range(len(height)):
for j in range(len(height)):
if j > i:
l = j - i
h = min(height[i], height[j])
area = l * h
if area > m: m = area
return m
Golang Implementation
func maxArea(height []int) int {
max_so_far := 0.0
for i := 0; i < len(height); i++ {
for j := 0; j < len(height); j++ {
height := math.Min(float64(height[i]), float64(height[j]))
width := j - i
vol := height * float64(width)
max_so_far = math.Max(max_so_far, vol)
}
}
return int(max_so_far)
}
双指针,greedy
指针分别放在两端不断向中心靠近。
Time Complexity: 只需 iterate 一次�。
Space Complexity:
如何选择移动的指针
移动的那个必须是当前的min。
Area 由宽度和高度决定,高度是当前 2 个指针的 min。
当指针在向中心移动时,宽度一定在缩小,若想让 area 变大,只能希望高度变高。
Case 1: 移动 height 为 min 的指针
移动后,宽度一定变低,如果移动的不是 height 为 min 的指针,高度永远不可能变高。如果移动的是 height 低的那个,则有可能最终达到高的那个的 height。
Case 2: 当 2 个指针所指高度相同时,随机选一个
不论移动那个指针,下一步的 min height 都不可能超过当前的 height。
不论移动的是哪个,宽度都缩小了,高度都不会变,因为下一次的 Area 由两个指针的 min height 决定,而当前 2 个指针高度相同,下次的 min height 是 at most 当前的高度。所以当前移动一次之后 area 一定变小。就算之后 area 会增加也是之后几步希望 2 个指针都移动到更高的 height 上。
既然如果 area 要变大的话 2 个指针都必然会移动,那么当前移动那个一个就不重要了。 因为这算是一个 Greedy Algorithm,我们每一步只需要 care 当前的最优解就好了。
class Solution:
"""
Runtime: 128 ms, faster than 86.21% of Python3 online submissions for Container With Most Water.
Memory Usage: 15.4 MB, less than 35.33% of Python3 online submissions for Container With Most Water.
"""
def maxArea(self, height: List[int]) -> int:
m, s, e = 0, 0, len(height) - 1
while s != e:
area = (e - s) * min(height[s], height[e])
if area > m: m = area
if height[s] < height[e]:
s += 1
else:
e -= 1
return m
Go Implementation
func maxArea(height []int) int {
m, s, e := 0.0, 0, len(height) - 1
for s != e {
area := float64(e - s) * math.Min(float64(height[s]), float64(height[e]))
m = math.Max(m, area)
if height[s] < height[e] {
s++
} else {
e--
}
}
return int(m)
}